BAB
2 METER ARUS TERUS
2.1 :
BINAAN DAN FUNGSI METER MKGB
2.2 :
METER AMPIAR A.T.
2.2.1 : METER AMPIAR A.T. ASAS
2.2.2 : METER AMPIAR A.T. BERBILANG
JULAT
2.2.3 : KESAN SISIPAN METER AMPIAR
2.3
: METER VOLTAN A.T.
2.3.1 : METER VOLTAN A.T. ASAS
2.3.2 : METER VOLTAN A.T. BERBILANG
JULAT
2.3.3 : KESAN BEBAN METER VOLTAN
2.4
: METER OHM
2.4.1 : METER OHM SAMBUNGAN SIRI
2.4.2 : METER OHM SAMBUNGAN SELARI
2.4.3 : METER OHM BERBILANG JULAT
2.1
BINAAN DAN FUNGSI METER MKGB
Meter
pesongan yang didapati sekarang adalah jenis meter Magnet Kekal Gelung
Bergerak
(MKGB) atau dikenali meter d’Arsonval iaitu
instrumen elektromagnetik. Meter MKGB adalah meter
untuk mengukur arus terus dalam unit µA
atau mA. Dengan melakukan modifikasi, meter MKGB
boleh digunakan untuk mengukur arus dan
voltan (at dan au) dengan julat yang lebih besar dan boleh
juga direkabentuk bagi pengukuran rintangan.
Rajah
2.0 menunjukkan binaan meter asas MKGB:
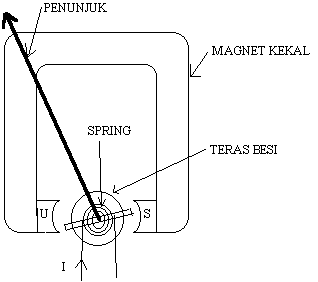
Rajah 2.0
magnet kekal yang berbentuk ladam kuda dengan
2 besi lembut yang bertindak sebagai
kutub utara dan selatan
teras dari besi lembut berbentuk selinder
terletak antara dua kutub
wayar halus dibelitkan pada satu kerangka
logam yang ringan yang diletakkan disekeliling
teras dan ia boleh berputar dengan bebas
penunjuk dilekatkan pada gelung bergerak
dan ia akan terpesong bila gelung berputar.
Operasi:
arus yang hendak diukur dialirkan melalui
lilitan gelung bergerak
gelung akan menjadi elektromagnet yang
mempunyai kutub-kutub utara dan selatan
interaksi diantara kutub-kutub magnet kekal
dengan kutub-kutub yang terbentuk menyebabkan
gelung akan berputar
penunjuk akan bergerak diatas skalar jika
arus mengalir arah yang betul.
2.2
METER AMPIAR A.T.
2.2.1
METER AMPIAR A.T. ASAS
Litar meter ampiar asas di Rajah 2.1
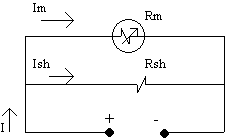
Rajah 2.1
di mana:
Rm : Rintangan dalam meter MKGB
Rsh : Perintang pirau (shunt)
Im : Ipsp : Arus pesongan skala penuh meter
MKGB
Ish : Arus pirau
I : Arus pusingan skala penuh meter ampiar
(julat meter ampiar)
Fungsi Rsh: meninggikan julat arus yang
boleh dibaca oleh meter dan memberi jalan altenatif
kepada arus I, ini akan melindungi meter
MKGB dari arus tinggi.
Analisis litar:
Vm = Im Rm, Vsh = Ish Rsh
Vsh = Vm
Faktor pekali (n) menunjukkan arus I yang
diukur bernilai n kali arus Im atau
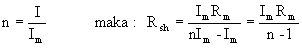
Contoh:
Kira nilai perintang pirau yang diperlukan
untuk menukarkan meter MKGB 1mA dengan
rintangan dalam 100 kepada meter ampiar
0 - 100mA.
IM = 1mA
RM = 100
I = 100mA
ISH = I - IM
= 100 mA - 1mA = 99mA
IMRM
= ISHRSH
maka RSH = [1mA(100)]/99mA
= 1.01 #
Contoh:
Satu meter MKGB 100µA dengan rintangan
dalam 1k digunakan dalam meter
ampiar 0 - 100mA. Tentukan nilai perintang
pirau yang diperlukan.
2.2.2 METER AMPIAR
A.T. BERBILANG JULAT JENIS
PIRAU AYRTON
Rajah 2.2 meter ampiar berbilang julat jenis
pirau Ayrton. Rekabentuk lebih praktikal dan banyak
di pasaran
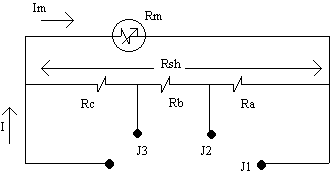
Rajah 2.2
Menentukan nilai setiap perintang pirau:
Dari litar:
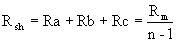
Pada julat J1:
Rsh = Ra + Rb + Rc selari dengan Rm, I1
= I - Im
I1 (Ra + Rb + Rc) = Im Rm
Pada julat J2:
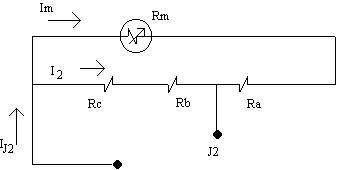
Rc + Rb selari dengan Rm + Ra, I2 = I -
Im
I2 ( Rc + Rb) = Im (Rm + Ra)
(**)
Pada julat J3:
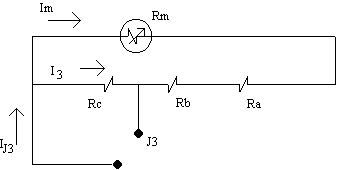
Rc selari dengan Rm + Rb + Ra, I3 = I -
Im
I3 (Rc) = Im (Rm + Rb + Ra)
Boleh gunakan kaedah penyelesaian persamaan
serentak bagi menentukan nilai Ra, Rb dan Rc
penyelesaian secara umum bagi mendapatkan
nilai Ra, Rb dan Rc iaitu dengan menyelesaikan
rumus (*) dan (**) akan menghasilkan:
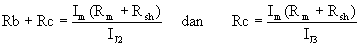
Contoh:
Kirakan nilai perintang-perintang pirau
Ra, Rb dan Rc
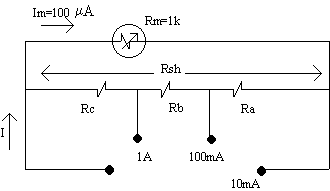
Rajah 2.3
RSH = Ra
+ Rb + Rc
n = I/IM
= 100
RSH = RM/n-1
= 1000/(100-1) = 10.1
Rc + Rb
= IM(RM RSH)/I2
= 0.0001(1000 + 10.1)/0.1
= 1.01
Rc = IM(RM
+ RSH)/I3
= 0.101 #
maka, Rb = 1.01 - 0.101
= 0.909 #
Ra = RSH - (Rc
+ Rb)
= 10.1 - 1.01 = 9.09 #
2.2.3 KESAN SISIPAN
METER AMPIAR
Semasa pengukuran meter ampiar disambung
secara siri dalam litar yang arusnya hendak
diukur. Meter ampiar mempunyai rintangan
dalam yang bernilai rendah bagi meter berjulat tinggi
(A) dan bernilai tinggi bagi yang berjulat
kecil (µA).
Menyisipkan meter aampiar dalam litar bermakna
menambahkan rintangan litar maka arus dalam
litar akan berkurangan.
a)
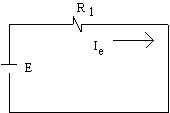
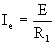
b)
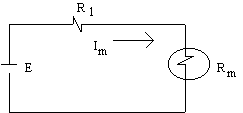
Rajah 2.4
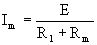
maka,
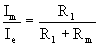
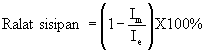
2.3
METER VOLTAN A.T.
2.3.1
METER VOLTAN A.T. ASAS
Litar asas binaan:
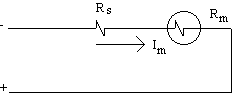
Rajah 2.5
Bagi membina meter voltan dengan julat
maksimum (V) tertentu, perintang Rs perlu ditentukan. Dari litar:
V
= (Rs + Rm) Im
Kepekaan meter ;

Maka:
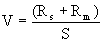
Jumlah rintangan meter volt :RT = (Rs +
Rm) = S x V = (kepekaan x julat)
Contoh:
Tentukan nilai rintangan pekali bagi meter
voltan a.t julat 50V yang menggunakan meter MKGB
500µA dan Rm = 1k
Penyelesaian : 50 V = ( Rs + 1k ohm ) 500
mikro A
Rs = 99k #
2.3.2 METER VOLTAN A.T.
BERBILANG JULAT
Rekabentuk sambungan perintang secara siri
lebih kerap digunakan secara komersial ialah:
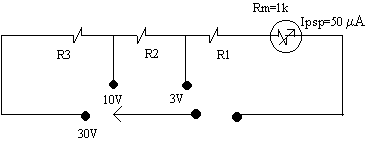
Rajah 2.6
Pada julat 3V:
3V = (R1 + 1k) 50µA
R1 = 59k #
Pada julat 10V:
10V = (R2 + 59k + 1k) 50µA
R2 = 140k #
Pada julat 30V:
30V = (R3 +140k + 59K + 1k) 50µA
R3 = 400k #
2.3.3 KESAN BEBAN METER
VOLTAN
Semasa
pengukuran meter voltan adalah disambung secara selari merentangi bahagian
yang hendak diukur . Kesan meletakkan
meter voltan ini mengurangkan voltan merentangi
bahagian tersebut. Ini adalah kerana meter
voltan mempunyai rintangan dalamnya tersendiri.
Kesan ini dipanggil kesan bebanan meter
voltan. Kesan beban ini bergantung kepada kepekaan
meter dan julat meter atau jumlah rintangan
dalam meter itu sendiri.
Contoh:
Dua buah meter voltan iaitu meter A dan
meter B digunakan untuk mengukur voltan merentangi
perintang R2 (Rajah 2.7). Meter-meter tersebut
mempunyai spesifikasi :
Meter A : S = 1k/V , Rm = 0.2k, Julat :
10V
Meter B : S = 20k/V , Rm = 1.5k, Julat :
10V
Kirakan:
Voltan merentangi R2 tanpa disambung dengan
meter
Voltan merentangi R2 apabila meter A digunakan
Voltan merentangi R2 apabila meter B digunakan
Ralat dalam bacaan meter voltan bagi setiap
meter
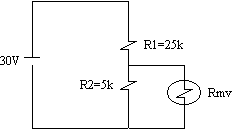
Rajah 2.7
(i) V merentangi R2 = [5/(25
+ 5)] x 30
= 5V #
(ii) RT = S x V
= 1000 x 10
= 10k
RS
= (5 x 10)/(5 + 10)
= 3.33k
VRB
= 30[3.33k/(25k + 3.33k)]
= 3.53V #
(iii) RT = S x V
= 20k x 10
= 200k
RS
= (5 x 200)/205 = 4.88k
VRB
= 30[4.88k/(25k + 4.88k)]
= 4.9V #
(iv) Ralat = [(5 - 3.53)/5] x 100% = 29.4% #
Ralat = [(5-4.9)/5]
x 100% = 2% #
(JWP: 5V, 3.53V, 4.9V, 29.4%, 2%)
2.4
METER OHM
2.4.1 METER OHM SAMBUNGAN SIRI
Terdiri daripada bateri meter MKGB dan perintang
Litar asas seperti Rajah 2.8 menunjukkan
sebuah meter ohm sambungan siri
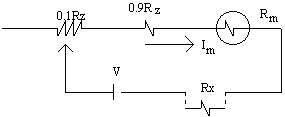
Rajah 2.8
Sebelum nilai Rx diukur, meter ohm biasanya
disifarkan terlebih dahulu.
Definasi ‘disifarkan’ : melitar pintaskan terminal
X-Y dan melaraskan Rz bagi menghasilkan
Ipsp pada meter MKGB
Ipsp = V/ (Rz + Rm)
Untuk mengukur Rx sambungkan ia pada terminal
X-Y;
I = V/ (Rz + Rm + Rx)
Hubungan antara pesongan meter daripada
skala penuh (P) dengan nilai Rx:
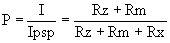
Contoh :
Suatu meter MKGB dengan pesongan skala
penuh 1mA digunakan dalam litar meter ohm.
Meter MKGB mempunyai rintangan dalam Rm
= 100. Bateri 3V digunakan dalam litar tersebut.
Tandakan permukaan meter untuk membaca
nilai perintang.
Jawapan :
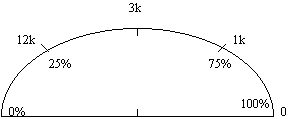
Skala meter ohm adalah sangat tidak linear.
Pada pesongan separuh skala penuh 50%,
didapati nilai Rx = jumlah rintangan dalam meter ohm
(RT = Rz + Rm)
Bagi pengukuran nilai rintangan yang kecil
Rx < 100 meter jenis sambungan ini tidak dapat
beroperasi dengan sebaiknya. Biasanya digunakan
jenis sambungan selari yang juga dipanggil
meter ohm pirau (shunt ohmmeter)
2.4.2 METER OHM SAMBUNGAN
SELARI
Contoh 1:
Litar asas meter ohm sambungan selari:
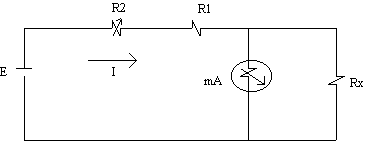
Rajah 2.9
Meter MKGB yang digunakan jenis mA atau
µA. R1 untuk menghadkan arus melalui meter
dan kebanyakan mungkin terdiri dari dua
perintang iaitu jenis boleh ubah dan yang tetap seperti di
litar iaitu R2 dan R1. Perintang boleh
ubah fungsinya sama sebagai pelaras sifar.
Biasanya R1Rm (R1 = 100 X Rm) supaya sebarang
perintang yang tidak diketahui apabila
disambung selari dengan meter akan mempengaruhi
arus yang kecil.
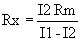
I1: arus apabila tiada sambungan perintang
Rx
I2: arus yang mengalir bila Rx disambung
antara terminal A-B
Contoh 2:
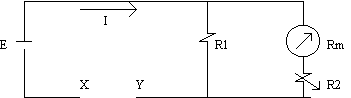
Rajah 2.10
Untuk membina meter Ohm jenis ini akan ditentukan
nilai R2 terlebih dahulu sebelum memilih
R1 yang bersesuaian. Fungsi R2 adalah sebagai
pelaras sifar. Caranya:
Jika Rm = 2kW , Im = 50m A dan E = 1.5V,
pintaskan XY (Rajah 2.11), maka R2 = 28kW
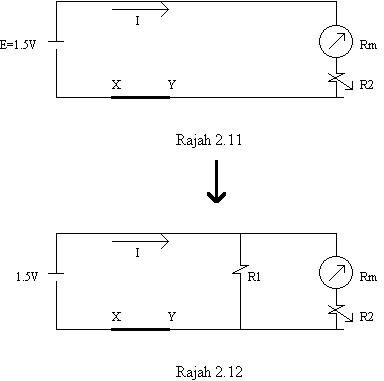
Pilih R1 jauh lebih kecil berbanding rintangan
Rm + R2 di atas dan sambungkan selari dengan meter
(Rajah 2.12).
Ini adalah kerana jika: R1 <<<<
( Rm + R2 ) supaya apabila R1 // ( Rm + R2 ) » R1
Contoh : ambil R1 = 10W
Pintaskan X-Y maka didapati pesongan adalah
100%. Kerana R1 <<<< ( Rm + R2 ) dan apabila
R1 // ( Rm + R2 ) » R1 , seolah-olah
rintangan keseluruhan meter adalah 10W
Jika pada X-Y diletakkan perintang 10W
didapati penunjuk akan terpesong 50%. Kerana
dengan andaian rintangan meter 10W di atas
maka:
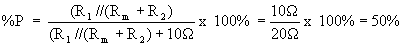
Ini membolehkan kita mereka meter Ohm untuk
mengukur nilai rintangan yang rendah dan seterusnya
meter Ohm berbilang julat.
2.4.3 METER OHM BERBILANG
JULAT
Binaan
meter Ohm berbilang julat berdasarkan Rajah 2.10. Berasaskan meter satu
julat ini dengan
data-data dari contoh yang telah dibincangkan,
rekabentuk meter berbilang julat (3 julat) ditunjukkan
dalam Rajah 2.13.
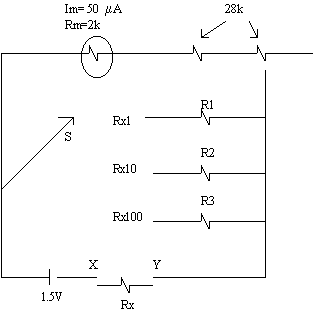
Rajah 2.13
Kaedah untuk mendapatkan Rz telah ditunjukkan
di atas. Pada Julat X1 iaitu merupakan julat asas
meter yang juga skala meter akan menunjukkan
pesongan 50% jika Rx yang diukur adalah 10 jika R1
yang digunakan adalah 10 (telah ditunjukkan
cara kerja). Dengan ini bagi menetukan R2 dan R3 adalah :
Jika S pada julat RX10: Jika pesongan penunjuk
50%, sedah pasti rintangan yang sedang diukur adalah
10 X 10 = 100. Nilai ini sama dengan jumlah
rintangan meter Ohm itu sendiri. Maka dari:
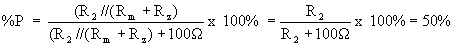
Nilai R2 adalah 100
Jika S pada julat RX100: Jika pesongan
penunjuk 50%, sudah pasti rintangan yang sedang diukur
adalah 10 X 100 = 1000. Dengan cara yang
sama dengan RX10, akan diperolehi nilai R3 yang diperlukan
adalah 1000.
KEMBALI KE MAIN PAGE