5.1
: Pengenalan
5.2
: Konsep Asas Tetimbang Wheatstone
5.3
: Binaan Tetimbang Wheatstone Dan Prinsip Keseimbangan
Tetimbang Wheatstone
5.4
: Litar Kepekaan Tetimbang Wheatstone
5.5
: Ketidakseimbangan Tetimbang Wheatstone
5.6
: Litar Setara Thevenin Tetimbang Wheatstone
5.7
: Titian Wheatstone Tak Seimbang
5.8
: Titian Kelvin
5.9
: Litar Kemudian Titian @ Bridge Control Circuit
5.10 :
Kegunaan Tetimbang Wheatstone
Litar tetimbang merupakan instrumen untuk mengukur nilai perbandingan dan
digunakan secara
meluas
untuk mengukur rintangan, aruhan, kemuatan, dan galangan (Z). Pengukuran
diukur dengan
kaedah
penunjukan sifar atau nol. Penunjuk tidak bergantung kepada peranti ukuran
atau calibration
dari
peranti penunjuk. Pengukuran melalui tetimbang ini adalah begitu tepat
dan jitu bagi sesuatu
parameter.
Litar titian juga digunakan dalam litar kawalan di mana terdapat satu lengan
titian yang
mengandungi
satu elemen rintangan yang sensitif pada parameter fizikal seperti suhu,
tekanan dan
lain-lain
yang sedang dikawal.
Tetimbang Wheatstone yang biasanya digunakan dalam pengukuran rintangan
direka dan
diperkenalkan
pada tahun 1833 oleh Samuel Christie. Kemudiannya, pada tahun 1847 Charles
Wheatstone
memperbaiki keupayaannya untuk kegunaan komersal. Tetimbang Wheatstone
merup
akan
alatan yang kejituan dan ketepatannya yang boleh dipercayai. Pengukuran
rintangannya
mempunyai
kejituan yang tinggi antara unit miliohm dan megaohm sehingga 0.1% berbanding
dengan
ralat
dalam alat meterohm bagi pengukuran rintangan antara 3% hingga 5%.
5.2 Konsep Asas Tetimbang Wheatstone
Tetimbang Wheatstone ialah tetimbang arus terus yang digunakan untuk mengukur
rintangan
suatu perintang atau bahan yang mengalami kesan perubahan rintangan yang
nilainya
tidak diketahui.
Kaedah nol atau konsep perbezaan keupayaan antara dua cabang dalam suatu
litar digunakan
dalam pengukuran. Kaedah ini berasaskan bahawa jika tiada perbezaan keupayaan
antara dua
cabang litar tetimbang yang selari, tidak akan ada sebarang pesongan pada
jarum
meter penunjuk
dan arus tidak mengalir melalui meter penunjuk dan menunjukkan bacaan sifar.
Ini menunjukkan
keadaan keseimbangan pada tetimbang dan biasanya galvanometer
disambungkan
di antara cabang selari untuk mengesan keadaan keseimbangan.
5.3 Binaan Tetimbang Wheatstone dan Prinsip Keseimbangan Tetimbang Wheatstone
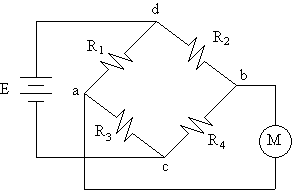
Rajah 5.1 menunjukkan binaan Litar Tetimbang Wheatstone. Terdapat empat
buah perintang
yang
disusun seperti dalam rajah 5.1. Sumber bekalan kepada litar tetimbang
disambung antara
punca
d dan c iaitu bekalan kuasa arus terus (E). Metergalvano disambung diantara
punca a dan b.
Arus
yang mengalir di galvanometer ialah Ig=0. Oleh itu, tetimbang diseimbangkan
yang bermaksud
voltan
di R3 = voltan di R4.
\
V3 = V4
\
I3R3 = I4R4
(1)
Pada ketika titian keseimbangan, voltan susutan di R1 = R2.
\ I1R1 = I2R2 (2)
Oleh sebab tiada pengaliran arus di galvanometer pada ketika keseimbangan,
I1 = I2
Dan
I2 = I4
Gantikan I1 = I3 dan I2 = I4 dalam (1):
I1R3 = I2R4 (3)
Persamaan (2) dibahagi dengan (3):
R1/R3=R2/R4
\ R1R4 = R2R3 (4)
Persamaan (4) ialah persamaan bagi tetimbang dalam keseimbangan.

Rajah 5.1 Tetimbang Wheatstone
Litar Tetimbang Wheatstone digunakan untuk mengukur nilai rintangan perintang
dengan kaedah
keseimbangan
nol. Biasanya perintang R4 dijadikan Rx
yang hendak dicari. Jika Rx menjadikan
tetimbang
tidak seimbang, perintang bolehubah R3 dilaraskan
sehingga metergalvano mencapai
keseimbangan.
Contoh
5.1
Cari
nilai rintangan Rx. Anggap Ig = 0.

R1 = 800 ohm
R2 = 900 ohm
R3 = 1k ohm
Rajah
5.2 Tetimbang Wheatstone
Penyelesaian
RxR1
= R2R3
R2R3
Rx
= R2R3/R1
= 900x1000 / 800
= 1125 ohm
5.4
Litar Kepekaan Tetimbang Wheatstone
Semasa Tetimbang Wheatstone pada keadaan ketidakseimbangan, arus mengalir
melalui
metergalvano dan menyebabkan pesongan pada penunjuk meter. Kepekaan tetimbang
ditentukan
untuk mengesan kuantiti arus yang melalui meter dan melihat berapa sensitifnya
tetimbang
terhadap ketidakseimbangan.
Kepekaan , S = Pesongan jarum penunjuk metergalvano, D / Arus, I
D = S * I
Unit bagi kepekaan
adalah (mm/mA) atau (radian/mA) atau (darjah/mA).
5.5 Ketidakseimbangan Tetimbang Wheatstone
Ketidakseimbangan dalam sebuah litar tetimbang adalah apabila berlaku sebarang
perubahan
pada jarum penunjuk metergalvano. Pesongan ini disebabkan perbezaan nisbah
keupayaan
antara dua cabang tetimbang yang menyebabkan pengaliran arus melalui meter.
Dalam
keadaan ini persamaan (4) tidak dipatuhi dan kaedah litar Thevenin digunakan.
5.6 Litar Setara Thevenin Tetimbang Wheatstone
Voltan setara Thevenin diperolehi dengan mengeluarkan metergalvano dan
melitar
bukakan
litar antara punca a dan b.
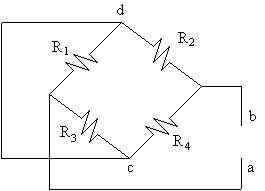
Rajah 5.3 Tetimbang Wheatstone tanpa metergalvano
Voltan di titik a: Voltan di titik b:
Va =
E [ R3 / R1 + R3
] ,
Vb = E [ R4 / R2 + R4
]
VTH = beza keupayaan di antara punca a dan b
VTH
= Va – Vb
= E { R3 / R1 + R3
}- E { R4 / R2 + R4
}
Rintangan setara Thevenin ditentukan melalui rajah dibawah.
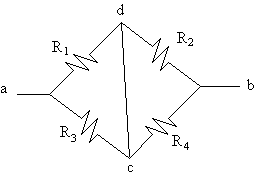
Rajah
5.4 Litar untuk mencari RTH
RTH
= R1 // R3 + R2
// R4
= [ R1R3 / R1
+ R3 ] + [ R2R4
/ R2 + R4 ]
Litar setara Thevenin Tetimbang Wheatstone adalah seperti berikut:
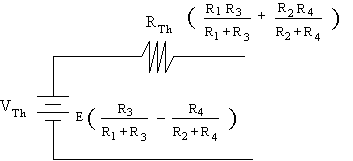
Rajah
5.5 Litar setara Thevenin
Nilai
VTH dan RTH yang diketahui dilukiskan
seperti berikut. Rintangan di antara punca a
dan
b ialah rintangan metergalvano iaitu Rg. Arus yang mengalir melalui metergalvano
ialah Ig.
Ig =
VTH / RTH + Rg
Contoh
5.2
Cari
arus yang melalui meter galvanometer , iaitu Ig
Rg =
200W

R1
= 10k ohm
R2
= 35k ohm
R3
= 40k ohm
R4
= 45k ohm
Rg
= 200 ohm
E
= 20 volt
Rajah
5.6 Tetimbang Wheatstone yang tidak seimbang
Penyelesaian
Cari
VTH:
VTH
= E { R3 / R1 + R3
}- E { R4 / R2 + R4
}
= 20 [ 40 / 40 + 10 ] - 20 [ 45 / 45 + 35 ]
= 20V (0.8 – 0.5625)
= 4.75 V
Cari RTH:
RTH
= [ R1R3 / R1
+ R3 ] + [ R2R4
/ R2 + R4 ]
= [ 10k x 40k / 10k + 40k ] + [ 35k x 45k / 35k + 45k ]
= 8k ohm + 19.6875k ohm
= 27.6875k ohm
= 27.6k ohm

Rg = 200 ohm
Rajah 5.7 Litar setara Thevenin
Cari Ig:
Ig =
VTH / RTH + Rg
= 4.75 V / 27.69k + 200
= 17.03 mA
5.7 Titian Wheatstone Tak Seimbang
Titian Wheatstone tak seimbang jika tiga daripada empat rintangan dalam
titian sama
nilai
R dan rintangan keempat berbeza daripada R sebanyak 5% atau lebih kurang.
Jika ini
berlaku
suatu sebutan anggaran yang tepat boleh dibuat untuk rintangan dan voltan
setara
Thevenin.
Voltan pada titik a: Voltan pada titik b:
Va =
E [ R / R + R ]
Vb = E [ R + r / R + R + r ]
= E / 2
Voltan setara Thevenin ialah perbezaan antara voltan a dan b:
VTH = Va – Vb = E [ R + r / R + R + r - 1/2 ] = E [ r / 4R + 2r ]
Jika
r 5% atau kurang dari nilai R maka ungkapan r dalam denominator boleh
digugurkan
tanpa wujud sebarang ralat. Untuk keadaan ini VTH adalah seperti berikut:
VTH = E [ r / 4R ]
Rintangan
setara dikira dengan menggantikan voltan bekalan kepada rintangan dalaman
atau
litar pintas dan litar dilukis semula dengan dilihat dari terminal a dan
b.
Rintangan Thevenin dikira sebagai
RTH = R / 2 + ( R )( R + r ) / R + R + r
Jika r terlalu kecil berbanding dengan R maka persamaan dimudahkan menjadi
RTH = R / 2 + R / 2 = R
Litar
setara Thevenin adalah seperti dalam rajah 5.10. Penghampiran ini adalah
98%
jitu
jika r < 0.05R.
Contoh
5.3
Cari
arus yang melalui metergalvano, Ig. Diberi Rg = 125W dan pergerakan tengah-sifar
200-0-200
mikro A.

R1=R2=R3= 500 ohm
R4 = 525 ohm
Rajah 5.8 Titian Wheatstone yang tidak seimbang
Penyelesaian
Cari
VTH:
VTH = E [ r / R ] = 10 x 25 / 2000 = 0.125 V
Cari
RTH:
RTH
= R = 500 ohm
Arus melalui metergalvano, Ig ialah:
Ig = VTH / RTH + Rg = 0.125 / 500 + 125 = 200 mikroA
Jika
pengesan metergalvano ialah 200-0-200 mikro A, dapat dilihat penunjuk terpesong
ke skala
penuh untuk perubahan 5% dalam rintangan.
5.8
Titian Kelvin
Titian Kelvin adalah pengubahsuaian daripada Titian Wheatstone. Tujuan
pengubahsuaian
ini adalah untuk menghapuskan kesan-kesan sentuhan (contact) dan
plumbum
(lead) pada rintangan apabila mengukur rintangan kecil yang tidak diketahui
nilai
Rx nya.
Rintangan dalam julat 1 ohm- 1 mikro ohm boleh diukur dengan darjah kejituan
yang tinggi
dengan
menggunakan Titian Kelvin. Oleh sebab Titian Kelvin menggunakan set ke-2
nisbah
lengan
seperti dalam rajah 5.12 maka ia kadang-kala dirujuk sebagai ‘Kelvin Double
Bridge’.
Rintangan, Rlc dalam rajah 5.12 menggantikan plumbum dan sentuhan rintangan
yang hadir
dalam
Titian Wheatstone. Set ke-2 dalam nisbah lengan (Ra & Rb) pada rajah
5.12 menggantikan
nilai
rintangan relatif yang rendah tersebut (low lead – contact).
Pada keseimbangan meter,
Ra /
Rb = R1 / R2
Pada
keadaan null, nilai Rx sama dengan Tititan Wheatstone,
Rx = R2R3 / R1
Oleh itu, pada ketika Titian Kelvin seimbang,
Rx / R2 = R3 / R1 = Ra / Rb
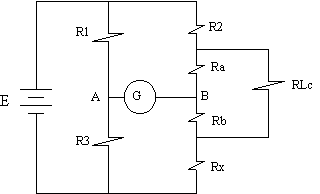
Rajah
5.9 Titian Kelvin
Contoh
5.4
Diberi nisbah Ra ke Rb ialah R1
= 10 ohm dan R1 = 0.5 R2 , cari
nilai Rx .
Penyelesaian
Cari
nilai Rx:
Rx
/ R2 = R3 / 10 = 1 / 2000
Oleh sebab R1 = 0.5 R2,
R2 = R1 / 0.5 = 10 / 0.5 = 20
Nilai Rx:
Rx = R2 / 2000 = 20 / 2000 = 0.01 ohm
5.9 Litar Kemudian Titian @ Bridge Control Circuit
Bezaupaya pada terminal keluaran akan wujud apabila terdapat ketidakseimbangan
dalam
titian. Bezaupaya ini menyebabkan arus mengalir dalam pengesan metergalvano
apabila
titian
digunakan dalam sebahagian dari peralatan ukuran.
Bezaupaya juga wujud apabila titian digunakan sebagai pengesan ralat atau
(error detector)
dalam
litar kemudian. Bezaupaya pada keluaran titian ini dipanggil isyarat ralat
(rajah 5.13).
 Isyarat
Ralat
Isyarat
Ralat
Rajah 5.10 Litar Tetimbang Wheatstone dengan isyarat ralat
Elemen litar pasif seperti tolak tarikan atau strain gauge, thermister
(rintangan yang
sensitif
pada suhu) atau photoresistor (rintangan yang sensitif pada cahaya), tidak
menghasilkan
sebarang
voltan keluaran.
Perubahan dalam rintangan hanya wujud apabila elemen litar pasif digunakan
sebagai salah
satu
lengan Titian Wheatstone kerana terdapat perubahan dalam parameter fizikal
yang peka atau
sensitif
(haba, cahaya dan tekanan).
Ini
menyebabkan titian tidak seimbang dan menghasilkan voltan keluaran atau
isyarat ralat.
Rintangan
Rv sensitif terhadap salah satu dari parameter isyarat fizikal yang berbeza
seperti
haba atau cahaya atau tekanan.
Jika nisbah
R2R3 / R1 = R2 / RV
Maka,
Rv = R1 / R3
Maka isyarat ialah = 0
Jika parameter isyarat fizikal berubah maka RV juga berubah. Ketidakseimbangan
wujud
dalam titian dan isyarat ralat wujud. Di dalam penggunaan kawalan, parameter
yang
dikawal
dan diukur diperbetulkan dengan meletakkan nilai Rv yang sesuai supaya
dalam keadaan
null
wujud pada keluaran titian.
Oleh sebab Rv berubah dalam jumlah yang kecil,
RTH = R
VTH
= E [ r / 4R ]
Contoh
5.5
Rintangan
Rv dalam rajah 5.15 sensitif terhadap suhu. Rajah 5.16 menunjukkan
kaitan
antara rintangan dan suhu.
Cari
a) Pada suhu berapakah titian menjadi seimbang.
b) Amplitud isyarat ralat pada 60°C
Suhu ( Darjah C )
20 40 60 80
Rintangan ( k ohm )
7 8 9
10
Rajah
5.16 Jadual rintangan melawan suhu
Penyelesaian
a) Nilai
Rv apabila titian seimbang dikira sebagai
Rv = R2R3 / R1 = 10k x 10k / 10k = 10k ohm
Titian seimbang apabila suhu 80°C. Nilai ini dibaca terus dari graf.
b) Daripada
graf, diketahui bahawa apabila suhu 60°C rintangan ialah 9kW. Oleh
itu, isyarat ralat,eg ialah
eg
= E [ R3 / R1 + R3
] - E [ Rv / R2 + Rv ]
= 12 [ 10k / 10k + 10k ] - 12 [ 9k / 9k + 10k ]
= 0.32 V
Isyarat ralat adalah :
eg = VTH = E [ r / 4R ]
di mana
r ialah 10k ohm - 9k ohm iaitu 1k ohm ,
eg
= 12 V x 1k / 40k = 0.025 V
5.10 Kegunaan Tetimbang Wheatstone
Tetimbang Wheatstone banyak kegunaannya. Salah satunya ialah mengukur rintangan
dc pelbagai
wayar bertujuan untuk mengawal kualiti wayar tersebut atau untuk mengawal
rintangan
transformer,
solenoid, atau ‘motor windings’.
Selain itu, syarikat telefon menggunakan Titian Wheatstone untuk mengenalpasti
kesilapan
(fault)
dalam kabel. Fault tersebut mungkin dua litar “shorted” atau pun satu litar
“shorted” ke bumi.
Kegunaan lain ialah sebagai penyesuai isyarat dalam sistem pengukuran.
Tetimbang juga
digunakan
dalam alat pengesan isyarat fizikal (sensor) seperti thermistor, tolok
terikan dan lain-lain
yang
mempunyai ciri perubahan rintangan terhadap perubahan parameter fizikal
yang dikesan seperti
suhu,
tekanan, daya dan sebagainya untuk mengeluarkan isyarat keluaran dalam
bentuk isyarat elektrik.
Di salah
satu lengan tetimbang akan ditempatkan sensor dan ketiga-tiga rintangan
lain adalah diketahui
nilainya.
Apabila perubahan pada parameter fizikal berlaku pada sensor yang diukur,
keadaan
ketidakseimbangan
terjadi. Oleh itu, perbezaan keupayaan akan wujud antara dua cabang tetimbang
dan
isyarat keluaran berbentuk isyarat elektrik akan diperolehi. Metergalvano
digunakan untuk
menentukan
magnitud arus yang terhasil itu. Dengan ini, hubungan antara parameter
fizikal dan isyarat
elektrik
diperolehi.