6.1      :   TITIAN SUDUT SAMA
6.2      :   TITIAN MAXWELL
6.3      :   TITIAN WIEN
6.4      :   TITIAN SUDUT BERLAWANAN
6.5      :   TITIAN SCHERING

 Titian arus ulangalik digunakan untuk mengukur induktan dan kapasitan. Kesemua titian ac berdasarkan kepada titian Wheastone.

       Galangan ada rintangan tulen dan galangan kompleks. Ia digunakan dalam anjakan fasa, membekalkan laluan suapbalik(feedback) untuk pengayun dan penguat(oslillators and amplifiers).Bila pengesan arus menjadi ‘null’
atau dalam keadaan seimbang dimana tiada arus mengalir dan tiada perbezaan voltan melintasi pengesan.

                           I1Z1 = I2Z2
                       Maka,
                         Z1/Z3 = Z2/Z4

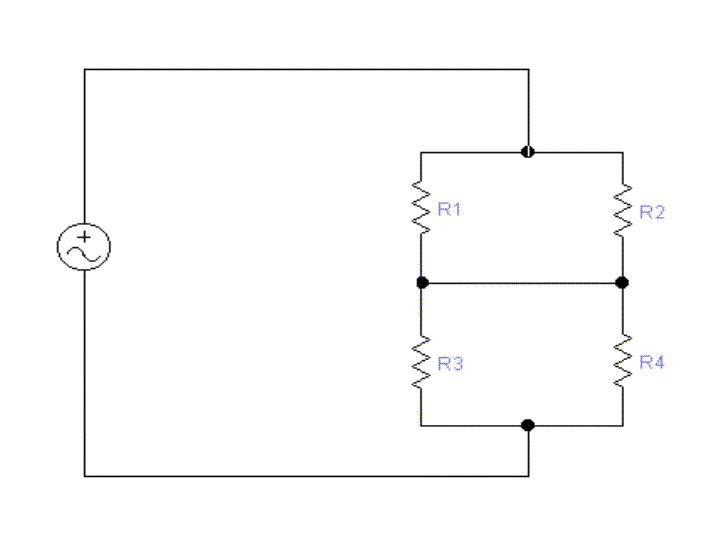
Contoh 6.1
Galangan ac bridge dalam litar di atas  diberi oleh
Z1= 200W Ð 30°
 Z2=150W Ð 0°
 Z3=250W Ð -40°
 Zx=Z4=?
Cari Zx.
Z1Zx  = Z2Z3
 Zx = (Z2Z3)/Z1 = 187.5W

Jumlah sudut yang diseimbangkan,
q1 + qx = q2 + q3
 qx = q2 + q3 - q1
 Zx = 187.5 W Ð -70°
     = 64.13 – j176.19W
Contoh 6.2
Merujuk rajah di atas, cari lengan yang tidak diketahui, Zx
R1 = 400W       R2 = W         L2 = 15.92mH
R3 = 300W       C3 = 0.4mF
w = 2pf = 2(p)(1000)Hz = 6283.19 rad/sec
XL = wL2 = 6283.19(15.92)(10-3) = 100W

Xc3 = 1/wc3 = 1/6283.19(0.4)(10-6)

Z1 = R1 = 400W Ð 0°
Z2 = R2 + jX2 = 200 + j100 = 223.6 Ð 26.6°
Z3 = R3 – jXc3 = 500Ð -53°
Zx = (Z2Z3)/Z1 = 279.5W Ð -26.4°
             = 250.35 – j124.28W
maka,
 C = 1/ wXc = 1/(6283.19)(124.28) = 1.28mF

Maka, rintangan adalah 250.35W dan kapasitan adalah 1.28mF

6.1 TITIAN SUDUT SAMA

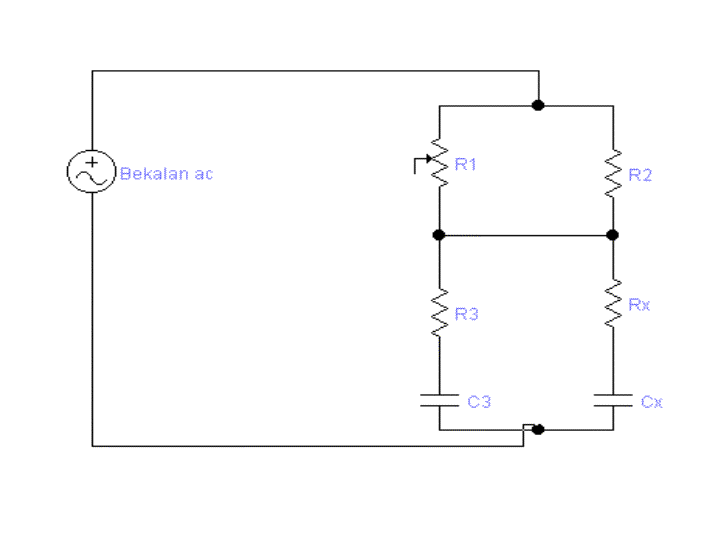
Kegunaannya – mengukur galangan dalam kapasitan
Z1 = R1
Z2 = R2
Z3 = R3 - jXcx
Untuk persamaan seimbang,
  R1(Rx – jXcx) = (R3 – jX3)R2
  R1Rx – jR1Xcx = R2R3 – jR2X3
Maka, persamaan seimbang,
R1Rx = R2R3
  -jR1Xcx = -jR2X3
  (-jR1)(1/wCx) = (-jR2)(1/wC3)
  R1C3 = R2Cx
Maka Rx dan Cx dicari,
Rx = (R2R3)/R1
Cx = (R1C3)/C3
Contoh 6.3
Titian sudut sama digunakan untuk mengukur ketakpastian pada frekuensi 2kHz. Pada keadaan seimbang,
titian adalah,
C3 = 100mF
R1 = 10kW
R2 = 50kW
R3 = 100kW
Cari galangan pada lengan tidak diketahui,
Rx = (R2R3)/R1 = 500kW
Cx = (R1C3)/R2 = 20mF
Titan sudut sama ini tidak bergantung kepada magnitud atau frekuensi voltan yang dikenakan.

6.2  TITIAN MAXWELL

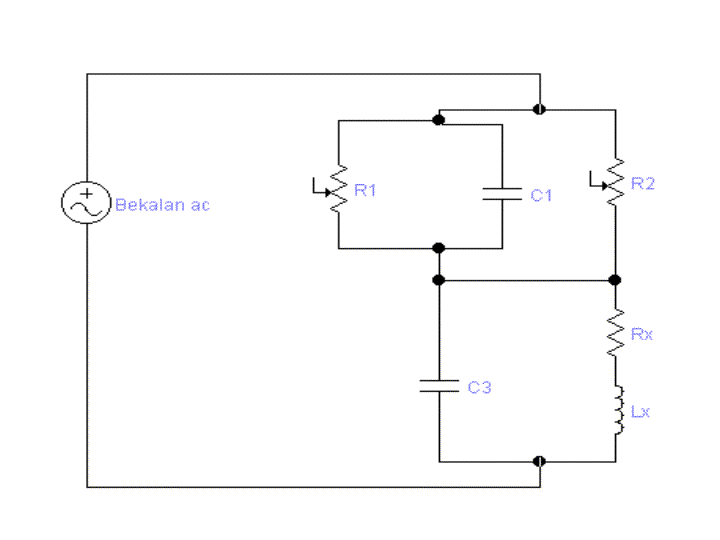
Dalam titian Maxwell,induktans yang tidak diketahui nilainya boleh diperolehi melalui piawai ketakpastian.
    Z1 = 1 / (1/R1+jwC1)
    Z2  = R2
     Z3 = R3
     Z4 = RX+jXLX

{1/[1/R1+jwC1]}(RX+JxLX) =R2R3
RX+JxLX = R2R3/R1+jwR2RC1
         RX = R2R3/R1
     JwLX = jwR2R3C1
         LX = R2R3C1

Contoh 6.4
Gunakan Titian Maxwell untuk mengukur induktans lengan.Titian pada keadaan seimbang adalah
          C1 = 0.01mF      R1 = 470 kW
          R2 = 5.1kW       R3 =100kW

    Cari RX dan LX
          RX = R2R3/R1  = 1.09kW
       LX  = R2R3C1 = 5.1H
 
 

6.3 TITIAN WIEN
Titian Wien digunakan untuk mengukur komponen galangan siri setara atau komponen galangan selari setara.

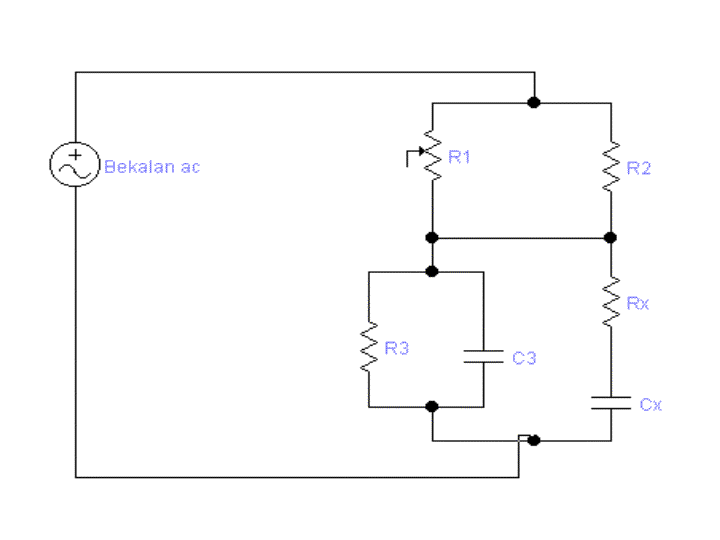
R3 = R1/R2 ( R4+1/w2R4C42)
C3 = R2/R1(1/1+w2R42C42)C4
R4 = R2/R1(1/1+w2R32C32)
C4 = R1/R2 (C3+1/w2R32C32)
 
 

Contoh 6.5
Cari R3 dan C3 menyebabkan galangan berikut pada keadaan seimbang.
R1   =  100kW                   R2  = 25kW
R4   =   3.1kW                  C4  =  5.2 mF
                                       F  =  2.5 kHz
w = 2pf  =  2p (2.5 x 103) = 15.71 x 103rad/sec
R3 = R1/R2(R4+1/w2R4C42)
      =  100 X 103/25 X 103(3.1 X 103 +1/(15.71 x 103)2(3.1 x 103)(5.2 x 10-6))
     =  4(3.1 x 103+ 1/20.65)
     =  12.4kW
C3 = R2/R1(1/1+w2R42C42)C4
     = 25 X 103/100 X 103
     = (1/1+(15.71 X 103)2(3.1 X 103)2(5.2 X 10-6)2)(5.2 X 10-6))
    = (1.3 X 10-6)(1/1+64132.07)
    = 20.3 pF

6.4 TITIAN SUDUT BERLAWANAN

Adalah digunakan untuk mengukur aruhan atau induktans.Nama lain untuk titian ini “Titian Hay”.Rangkaian ini
digunakan untuk mengukur rintangan dan aruhan di dalam gegelung di mana rintangan adalah kecil berbanding
dengan rengngan,XL.Ini bermakna,gegelung mempunyai nilai Q yang tinggi iaitu Q>10
                     Q>XL/R
Simbol Q bermaksud nisbah XL kepada R
RX = w2R1R2R3C1/1+w2R1C1
LX R2R3C1/1+w2R12C12

 

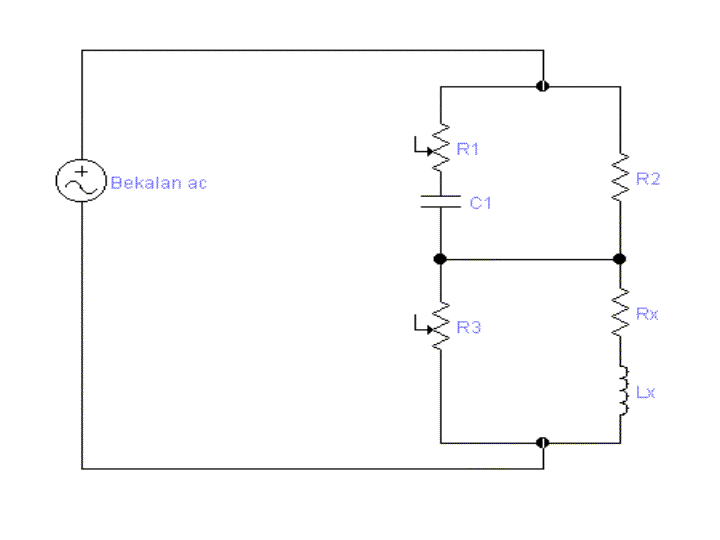
Contoh 6.6
Cari nilai RX dan LX pada keadaan seimbang dalam keadaan berikut.
W = 3000rad/s ,    R2 = 10kW  ,       R1 = 2kW
R3 = 1kW  ,      C1 = 1mf

RX = w2R1R2R3C12/1+w2R12C12
RX = (3 X 103)2(2 X 103)(10 X 103)(1 X 10-6)2/1+(3 X 103)2(2 X 103)2(1 X 10 –6)
     = 180 X 103/1+36
     = 4.86kW
LX = R2R3C1/1+w2R12C12
    = (10 X 103)(1 X 103)(1 X 10-6)/1+(3 X 103)2(2 X 103)2(1 X 10-6)2
   = 10/ 1+36 = 0.27 = 270 mH
RX = 4.86kW

6.5 Titian Schering
Titian Schering merupakan titian paling penting dan lebih baik berbanding titian lain.
Persamaan
Z1 = 1/R1+1/-jXC1       Z2  = R2
Z3 = jXC3                              Z4 = RX-jXX
 Z4 = Z2Z3/Z1 = R2(-JxC3)/1/1/R1+1/-JxC1
                               = R2(-jXC3)(1/R1-1/JXC1)
                     = R2(-j/wCx)(1/R1+jwC1)

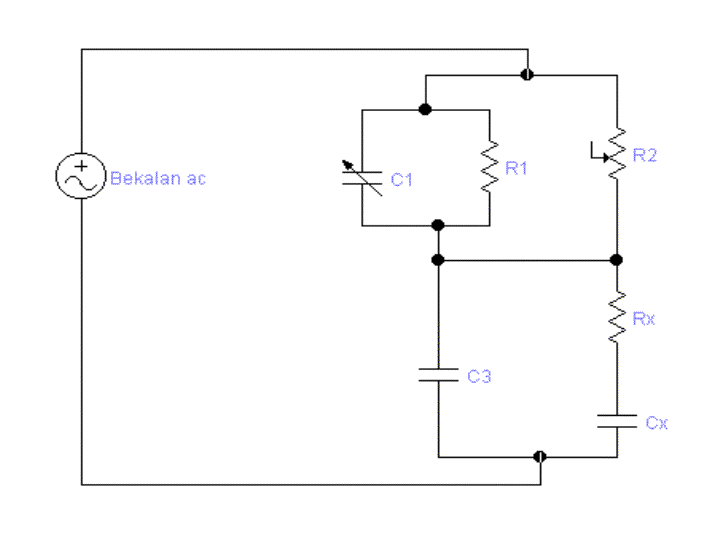
 RX = -j/wCx = R2C1/C3-Jr2/wC3R1)

RX = R2 C1/C3
CX = C3 R1/R2

Contoh 6.7
Cari RX dan LX dengan keadaan seimbang dengan galangan.
R1 = 470kW          C1 = 0.01mF
R2 = 100kW          C3 = 0.1mF
 

RX = R2C1/C3 = (100 X 103) (0.01 X 10-6)/(0.1 X 10-6) = 10kW
CX = C3R1/R2 = (0.1 X 10-6)(470 X 103)/(100 X 103) = 0.47 X 10-6F
                                                                                     = 0.47mF
 
 
 
 

                                                        KEMBALI KE MAIN PAGE